Hex to Binary Made Easy: A Step-by-Step Breakdown with Examples
Imagine you're deciphering a secret message, one where each symbol represents a hidden sequence of 0s and 1s. In the world of computers, this isn't just a fantasy—it's the reality of hexadecimal and binary systems. Hexadecimal, with its 16 characters (0-9 and A-F), and binary, the language of computers (0s and 1s), are fundamental building blocks of digital technology. Understanding how to convert between them is crucial for anyone working with programming, networking, or embedded systems. Let's dive into the fascinating world of hexadecimal to binary conversion and make it crystal clear.
What is Hexadecimal?:
Hexadecimal, often shortened to "hex," is a base-16 number system. This means it uses 16 distinct symbols to represent values. The familiar digits 0 through 9 are used, but we also need six additional symbols. For these, we use the letters A, B, C, D, E, and F, representing the decimal values 10 through 15, respectively.
- Visual Aid:
- A table comparing hexadecimal, decimal, and binary values:
| Hexadecimal | Decimal | Binary |
|-------------|---------|--------|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 1100 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
Why Hexadecimal?:
Hexadecimal is widely used in computing for several reasons:
- Compact Representation: It provides a more compact way to represent binary data. Each hexadecimal digit corresponds to four binary digits (bits), making it easier to read and write large binary values.
- Memory Addressing: It's used to represent memory addresses in computers.
- Color Codes: In web development and graphic design, hexadecimal is used to define color values (e.g., #FFFFFF for white).
- Data Representation: It is used to easily display binary data.
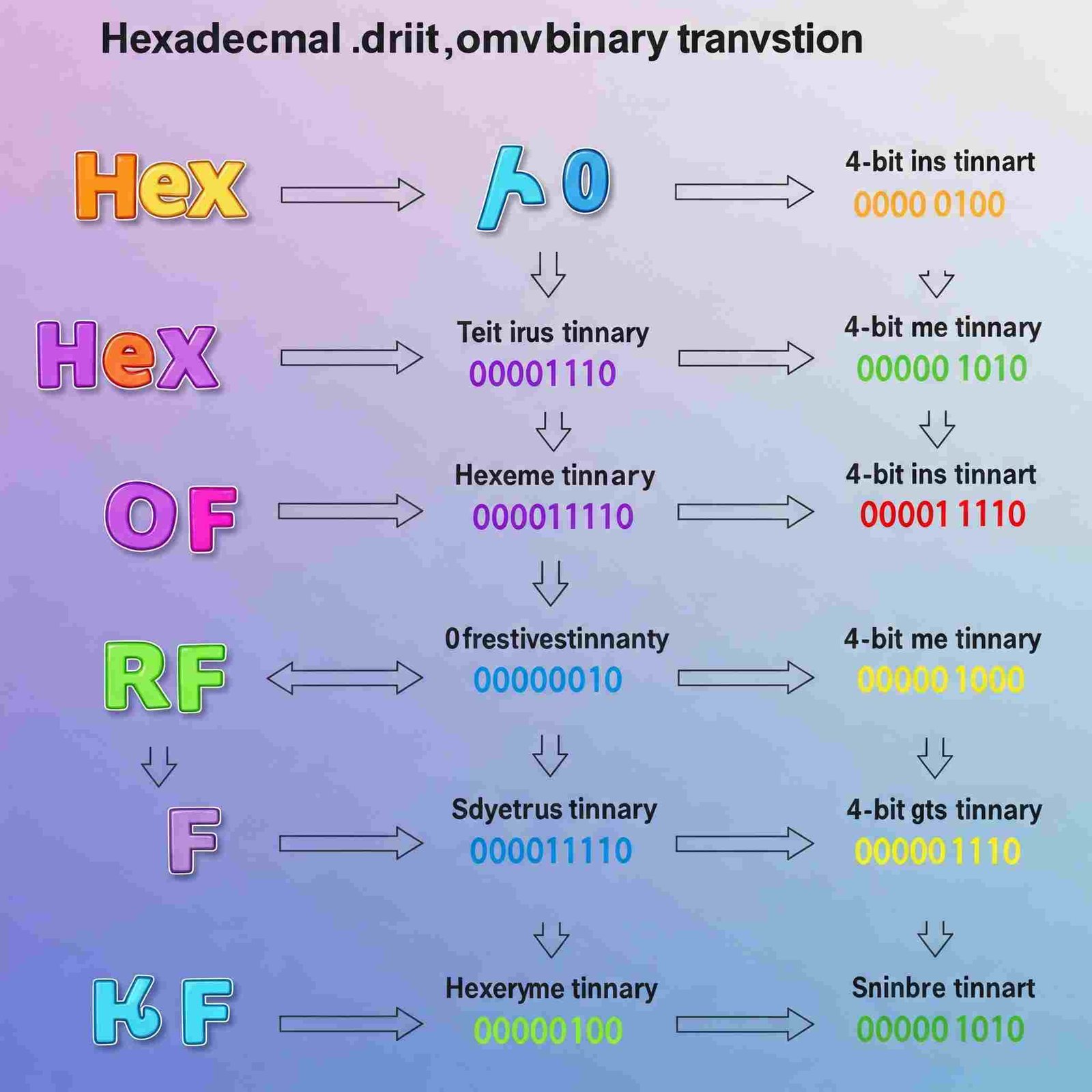
The Conversion Process: Hexadecimal to Binary (Step-by-Step Guide):
The conversion is straightforward:
- Look Up: For each hexadecimal digit, find its corresponding 4-bit binary equivalent from the table above.
- Combine: Concatenate the binary equivalents in the same order as the hexadecimal digits.
Example 1: Convert the hexadecimal value "2A" to binary.
- 2 in hex is 0010 in binary.
- A in hex is 1010 in binary.
- Therefore, 2A in hex is 00101010 in binary.
Example 2: Convert the hexadecimal value "1F" to binary.
- 1 in hex is 0001 in binary.
- F in hex is 1111 in binary.
- Therefore, 1F in hex is 00011111 in binary.
Visual Aid:
- Diagram showing the process of converting a hexadecimal number to binary, with arrows and clear labels.
Tips and Tricks:
- Memorization: Try to memorize the binary equivalents of the hexadecimal digits, especially the common ones.
- Grouping: When working with large binary numbers, group them into sets of four to make conversion to hexadecimal easier.
- Online Converters: Use online hexadecimal to binary converters for quick and accurate results, especially for complex conversions.
- Programming Languages: Many programming languages have built-in functions for hexadecimal to binary conversion.
Applications:
- Networking: IP addresses and MAC addresses are often represented in hexadecimal.
- Programming: Debugging code often involves examining memory dumps in hexadecimal.
- Web Development: HTML and CSS use hexadecimal color codes.
- Embedded Systems: Microcontrollers and other embedded devices use hexadecimal for memory management and data representation.
Conclusion:
Understanding hexadecimal to binary conversion is a valuable skill in the digital age. By grasping the basic principles and practicing regularly, you can confidently navigate the world of computer systems and data representation. Whether you're a programmer, a network engineer, or simply a tech enthusiast, this knowledge will empower you to unlock the hidden language of computers.